A New CMB Lensing Measurement with Two Years of SPT-3G Data

Yuuki Omori (KICP/UChicago)

mm-wave Universe 06/25/2025

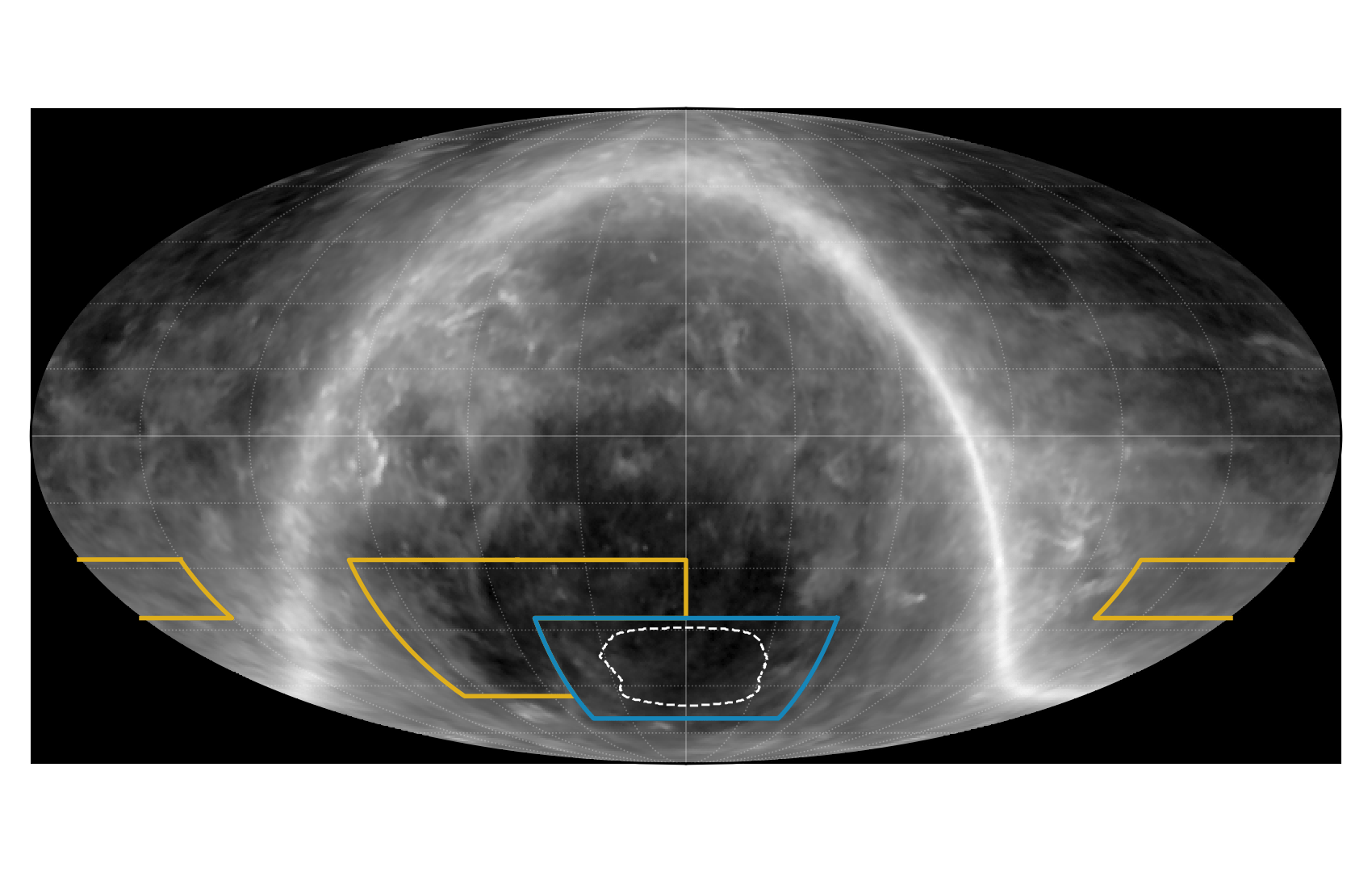
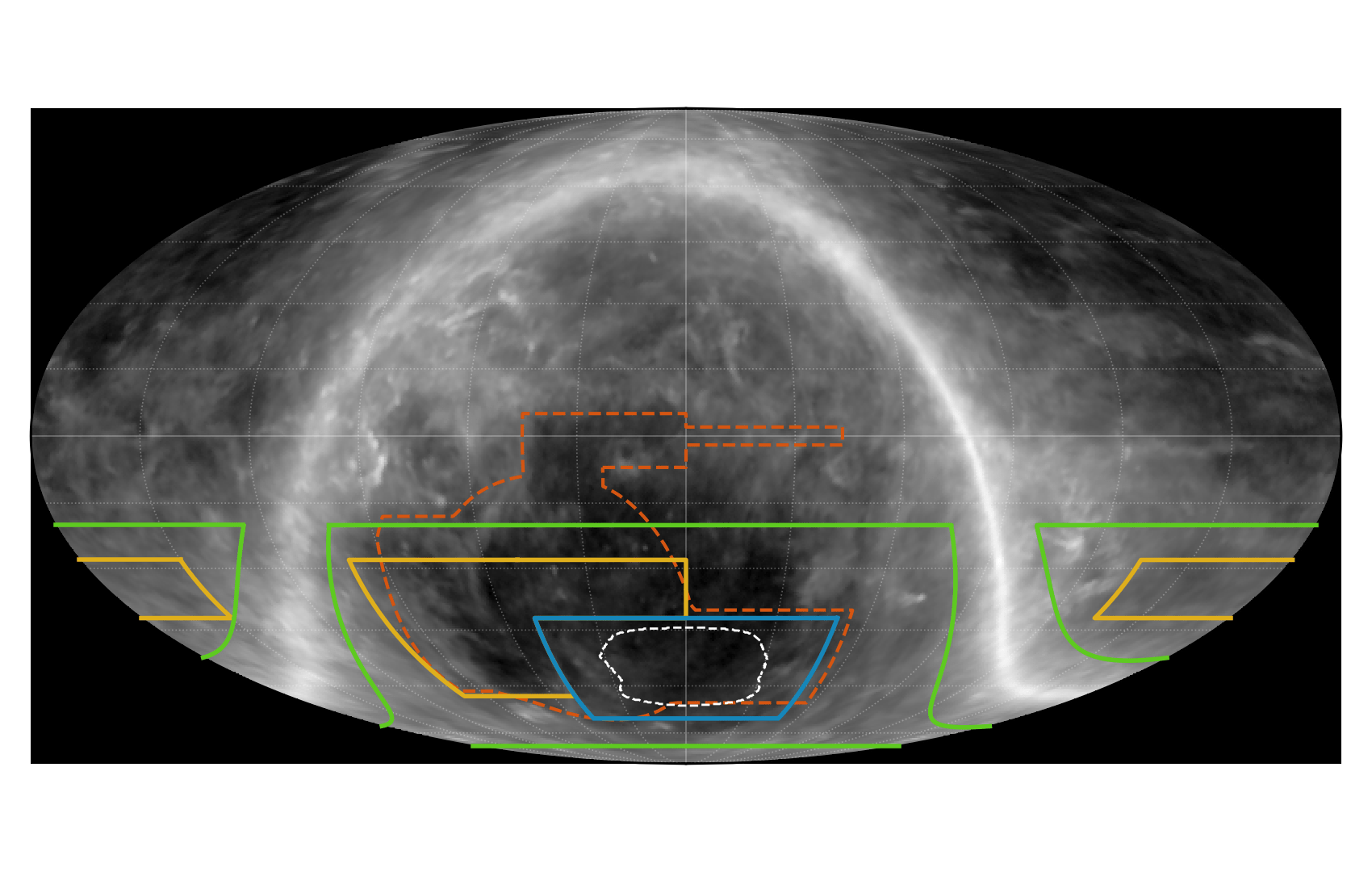
Wide field survey

SPT-3G Main 1500         field

{\rm deg}^{2}

See Wei's talk (9:00am Thurs)  for details on maps

See Etienne's talk (9:40am Thurs)  for details on TTEETE

W.L.K Wu

Y. Nakato

F. Bianchini

C. Daley

F. Ge

M. Millea

(SLAC > Caltech)

(SLAC)

(Stanford)

(Saclay)

(UCD)

(UCD)

QE (this work)

MUSE

SPT-3G lensing

See Fei's talk tomorrow at 9:20

Field-level forward modeling approach

P-only (T work in progress) 

Traditional quadratic estimator lensing reconstruction

(T+P) 

X^{d}(\vec{n})=X^{u}(\vec{n}+\vec{\alpha})\\
=X^{u}(\vec{n})+\vec{\nabla} X^{u}(\vec{n}) \vec{\nabla}\phi(\hat{n})\\
\langle X^{u}_{\ell m} (X^{u}_{\ell' m'})^{*} \rangle_{\ell\neq\ell',m\neq m'}=0
\langle X^{d}_{\ell m} (X^{d}_{\ell' m'})^{*} \rangle_{\ell\neq\ell',m\neq m'}=\sum_{LM}(-1)^{M}\begin{pmatrix} \ell & \ell' & L\\ m & m' & M \end{pmatrix}W^{\phi}_{\ell L \ell'}\phi_{LM}

Two independent modes become correlated through the lensing potential

\vec{\alpha}=\vec{\nabla}\phi(\hat{n})

Quadratic estimator

X\in \{T,Q,U\}

Lensing pipeline

Sign-flip noise

Raw sky 

Gaussian &

non-Gaussian

Mock skies

 

Filtering

Filtered lensing map

\bar{\phi}_{\rm NG}^{\rm sim}
\bar{\phi}^{\rm data}
\bar{\phi}_{\rm G}^{\rm sim}

Auto-spectra

Debiased bandpowers

Debiased bandpowers

Cosmological constraints

Data

ILC

N_{L}^{(0)},N_{L}^{(0),RD}
N^{(1)}_{L}
\mathcal{R}_{L}

x-corr 

Delensing

Mean-field

C^{-1}

Lensing

reconstruction

Combine  95/150/220 GHz

Can be tweaked to produce lensing map targeted for specific analyses

{\rm Convergence}\ (\kappa=-\frac{1}{2}\vec{\nabla}^{2}\phi)
{\rm Direction\ with\ more\ mass}
{\rm Direction\ with\ less\ mass}

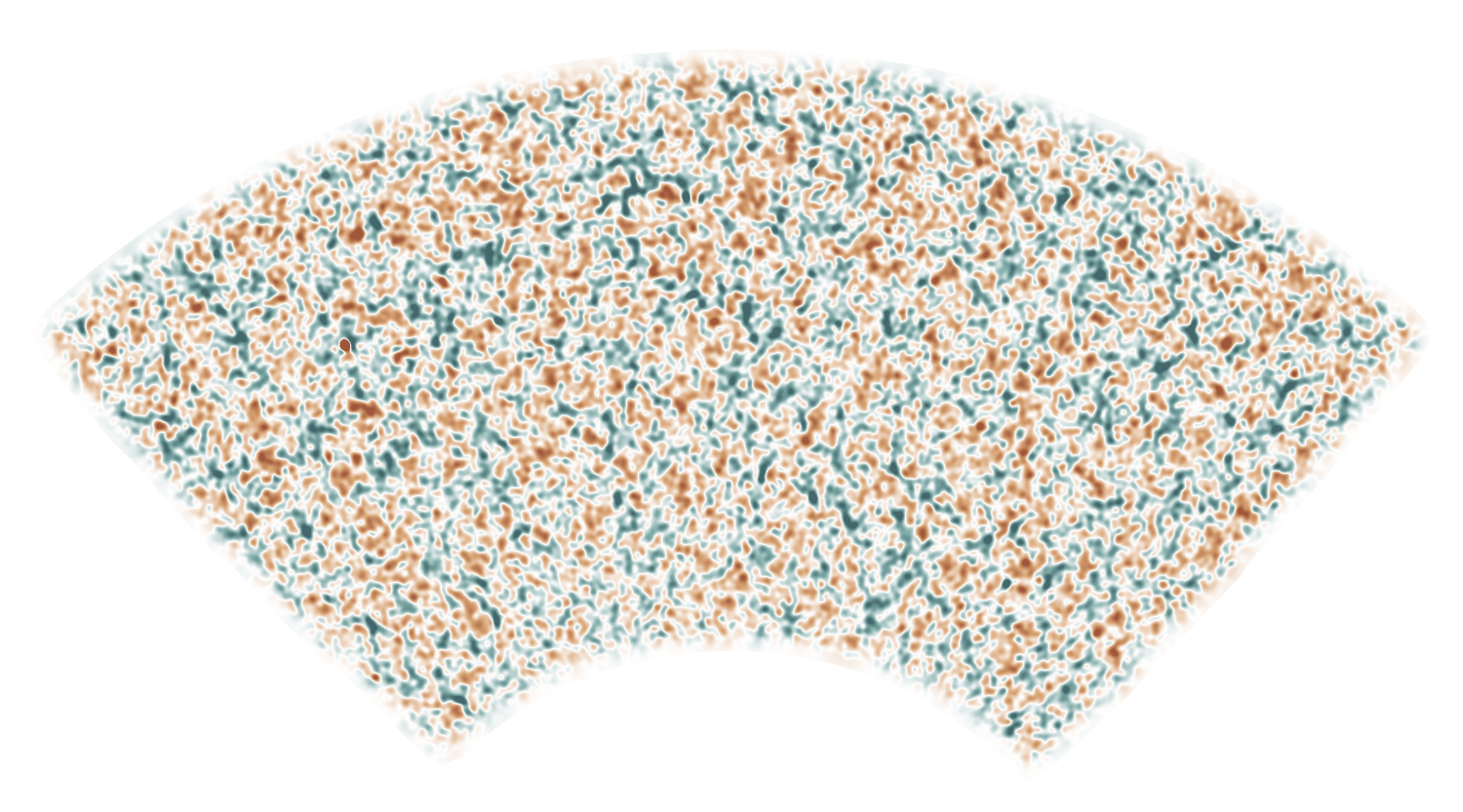
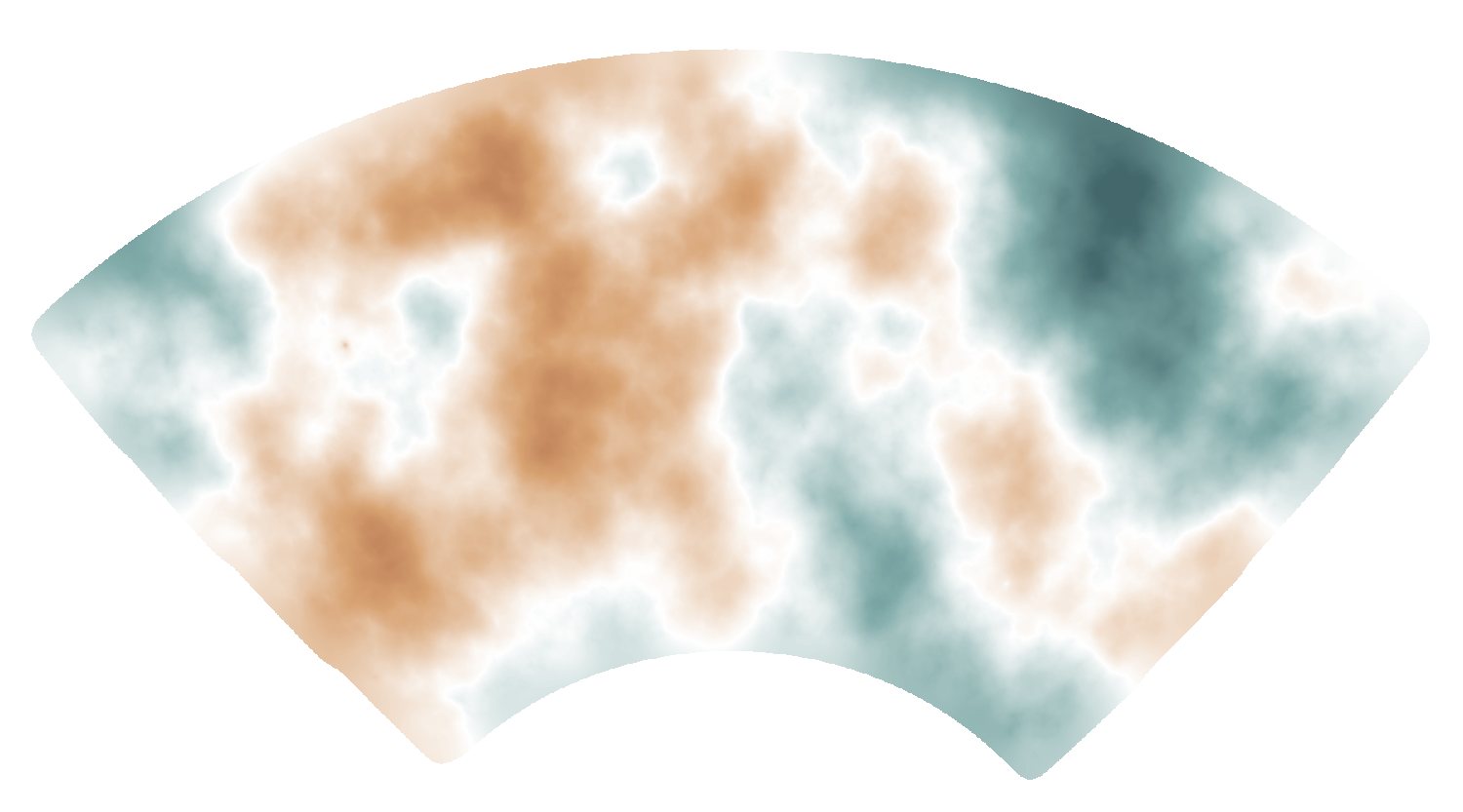
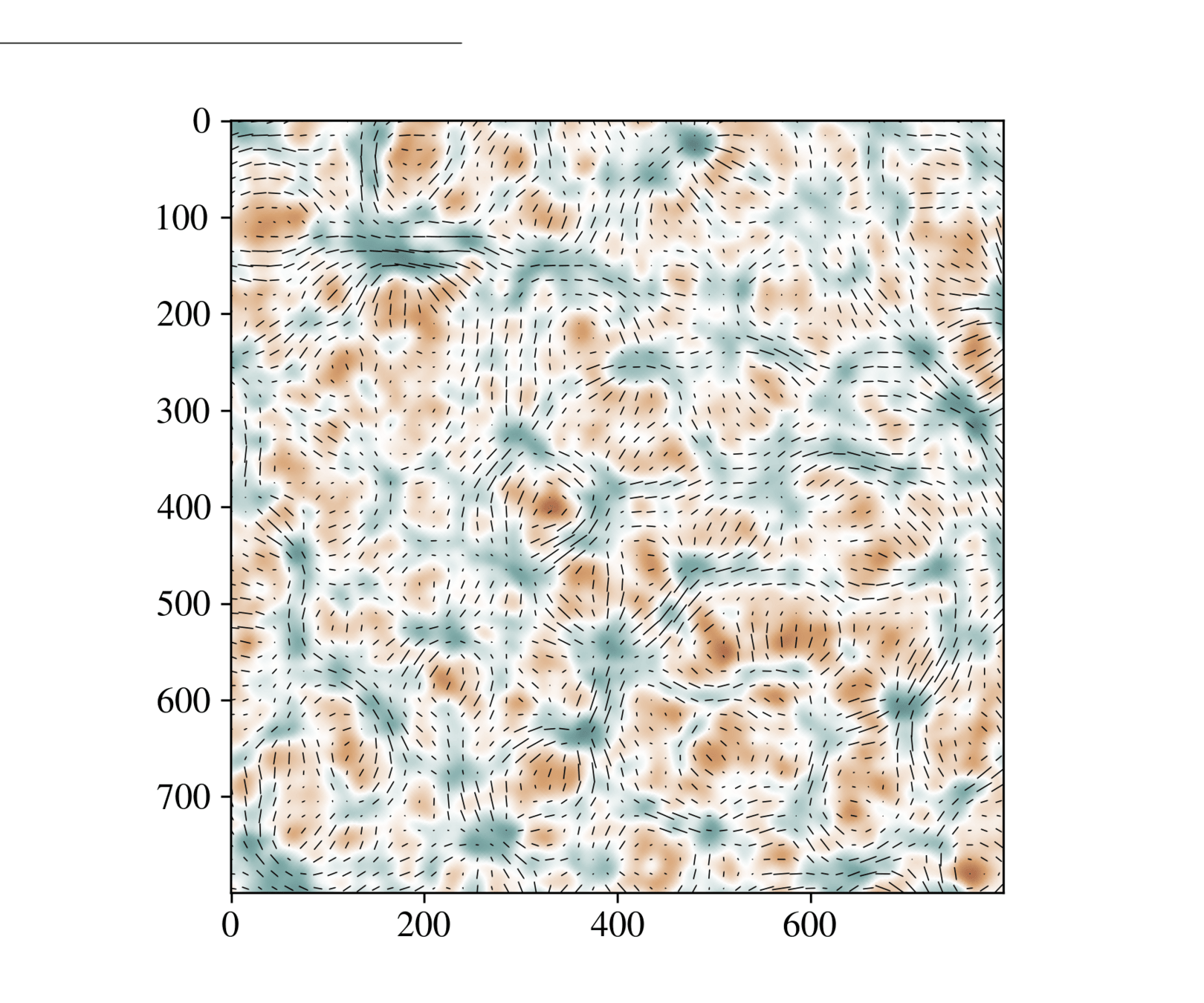
SPT-3G lensing map

(see also: Omori+ 2017, Omori+ 2023)

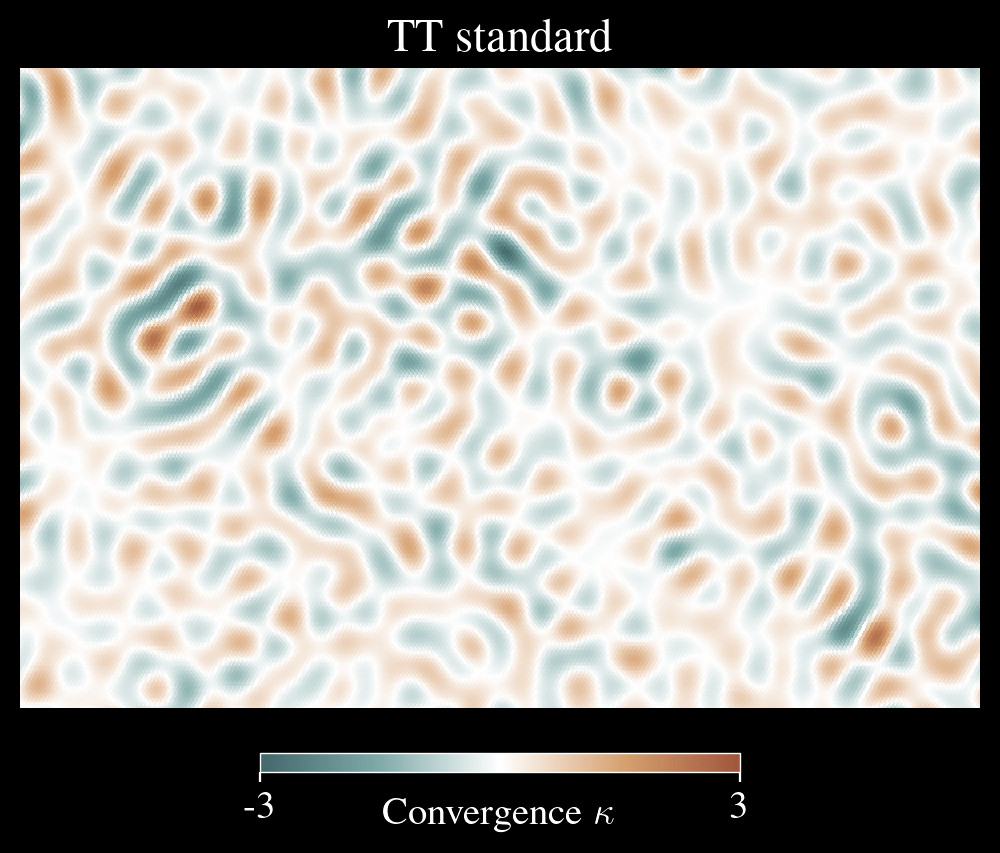
SPT-3G lensing - Maps

{\rm Lensing\ potential}\ (\phi)
{\rm Deflection}\ (\vec{\alpha}=\vec{\nabla}\phi)

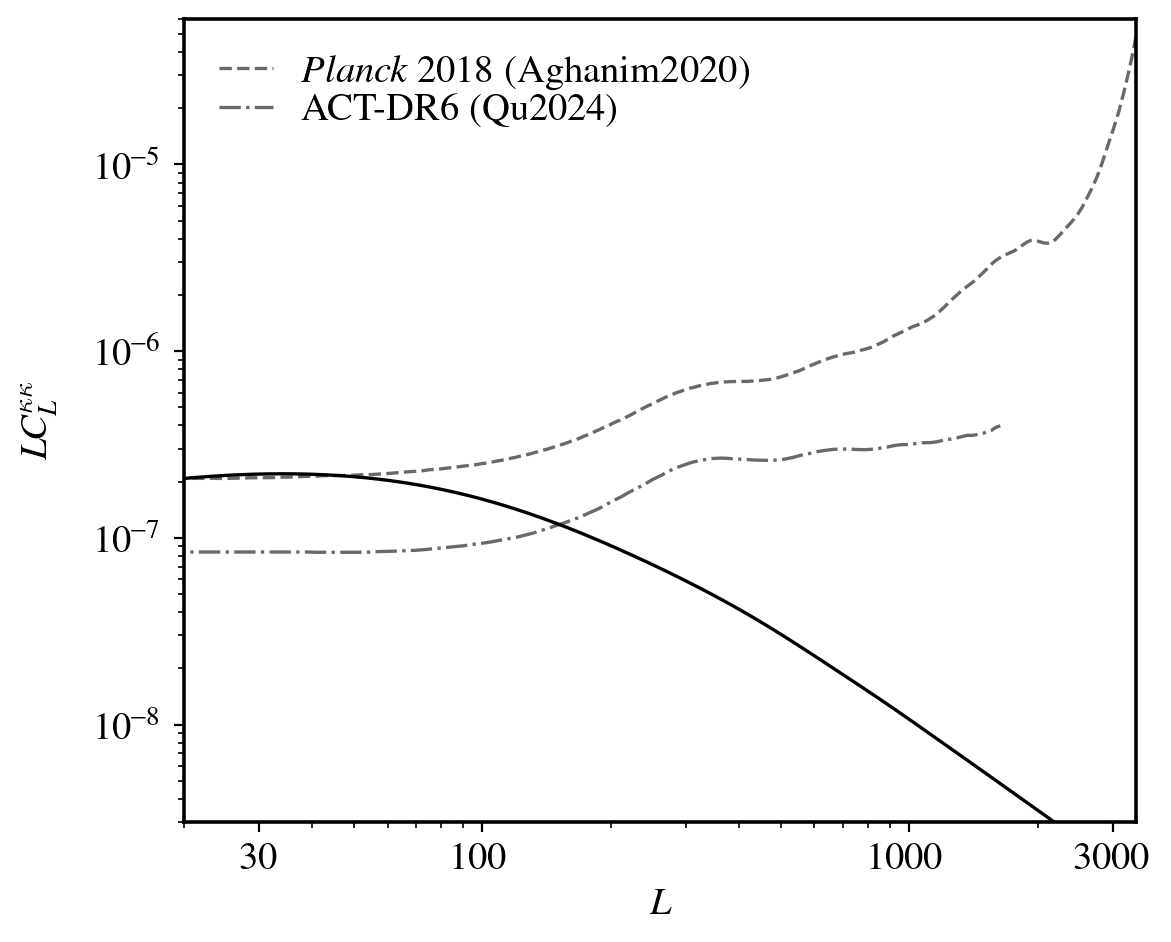
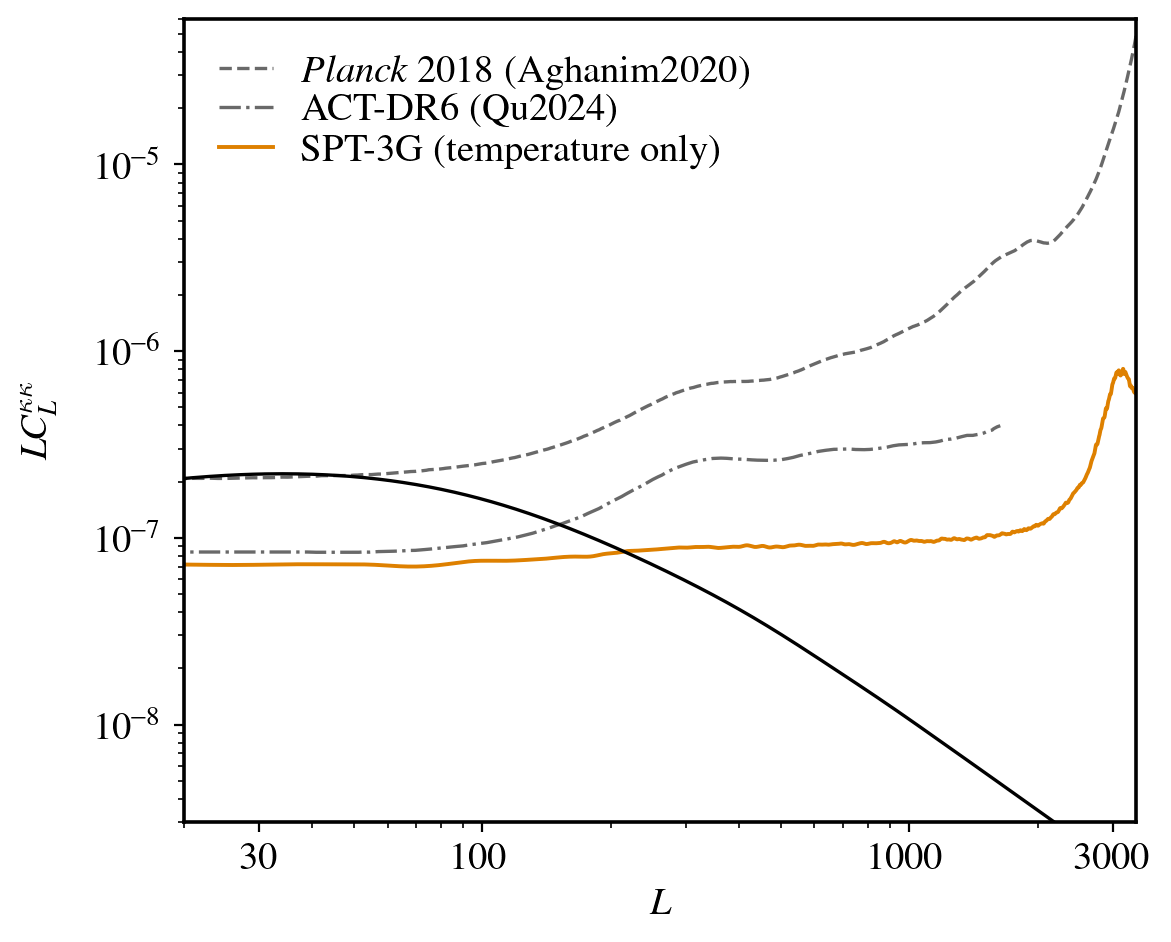
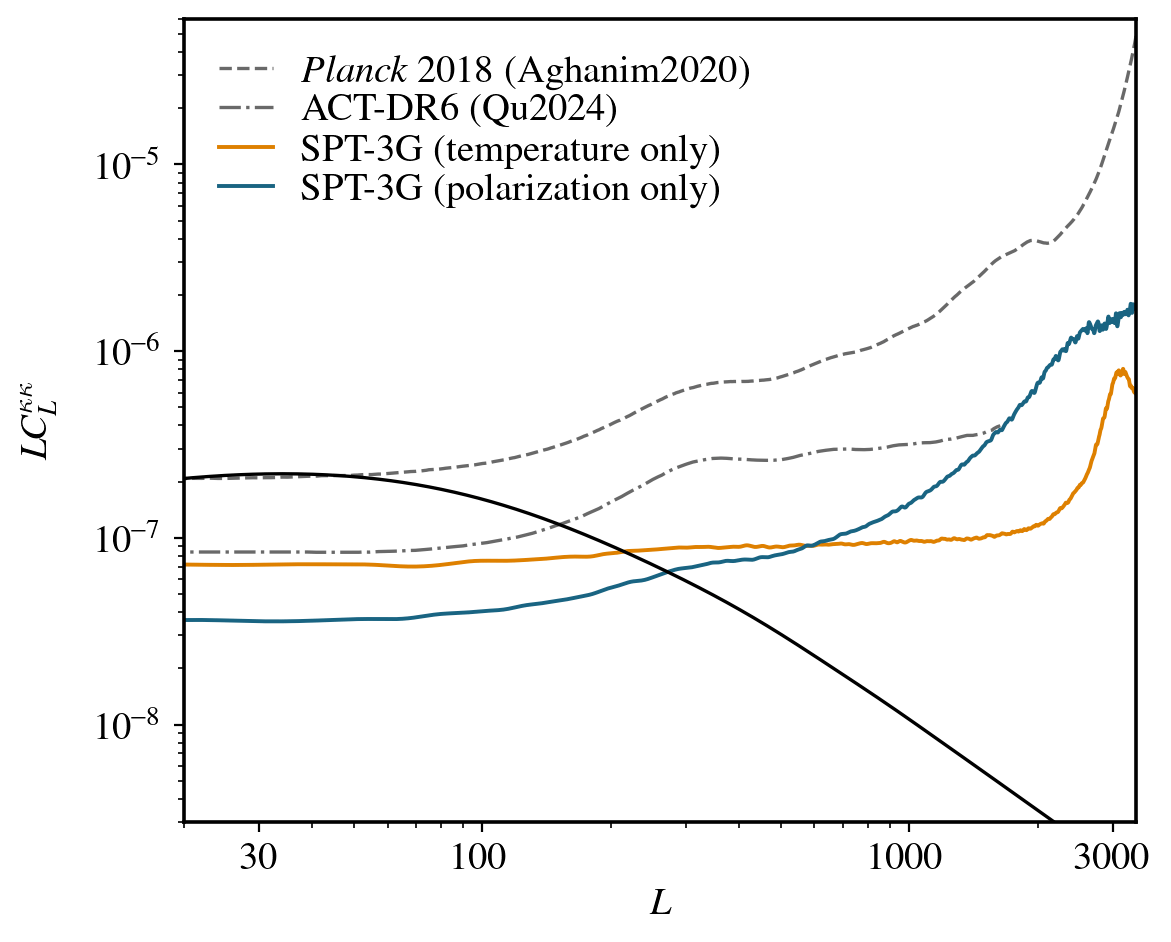
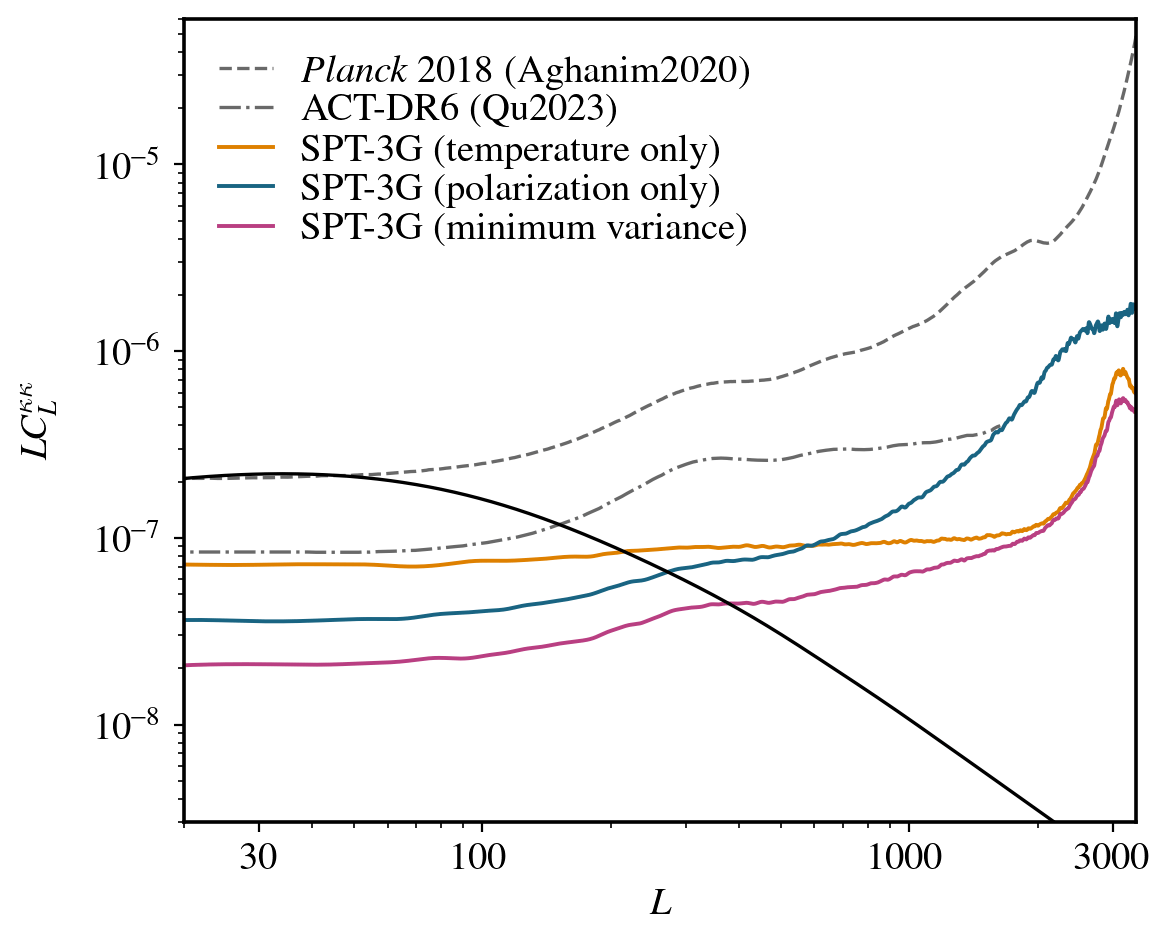
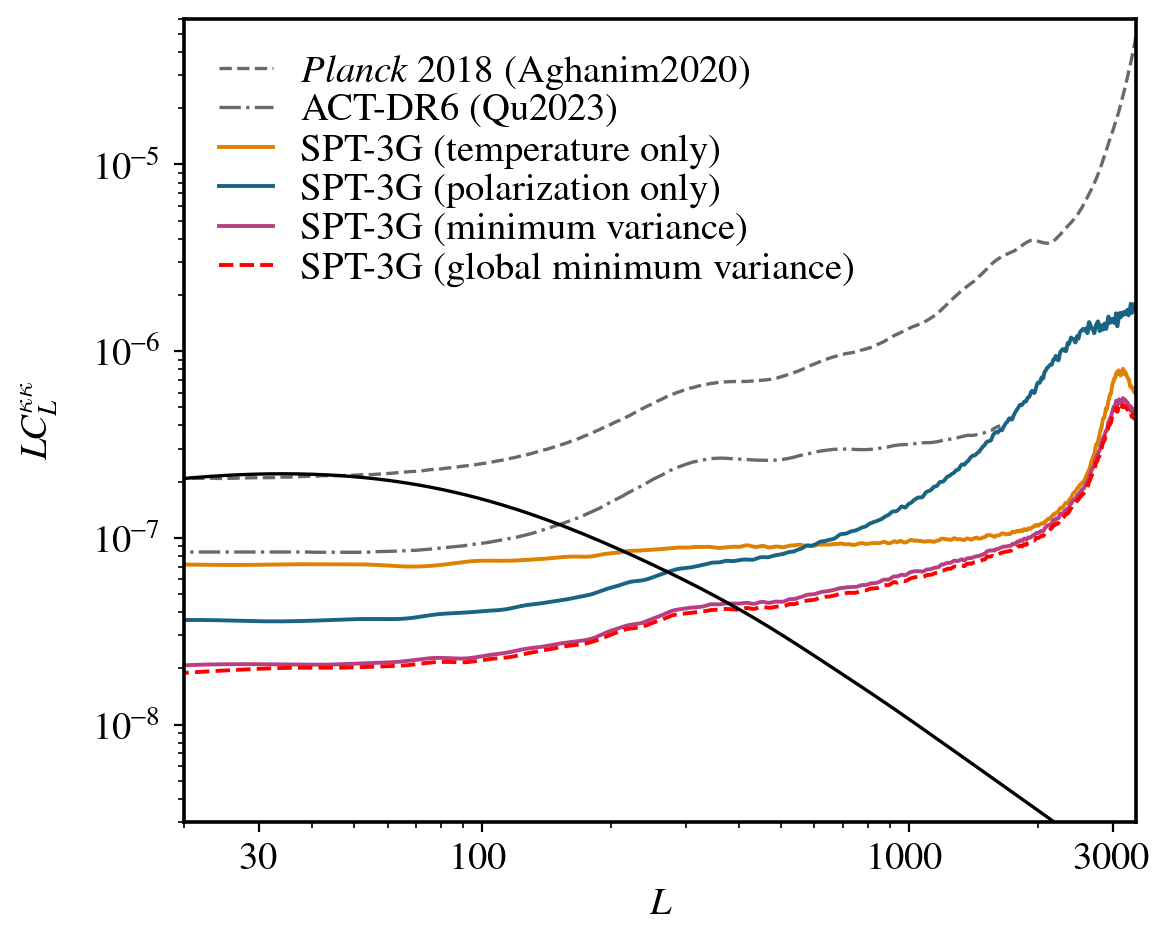
SPT-3G lensing - Noise levels

Lensing noise curves

Temperature

Polarization

Minimum 

variance

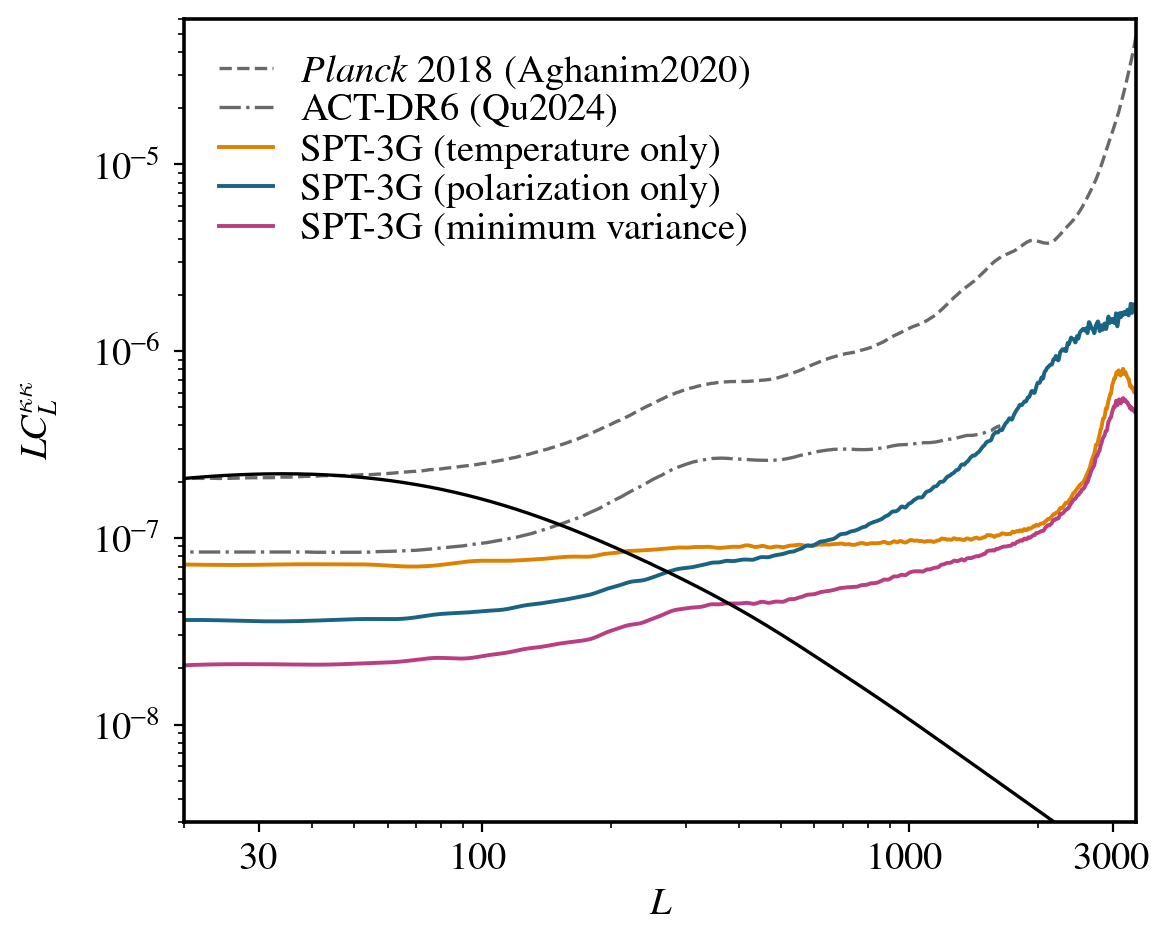
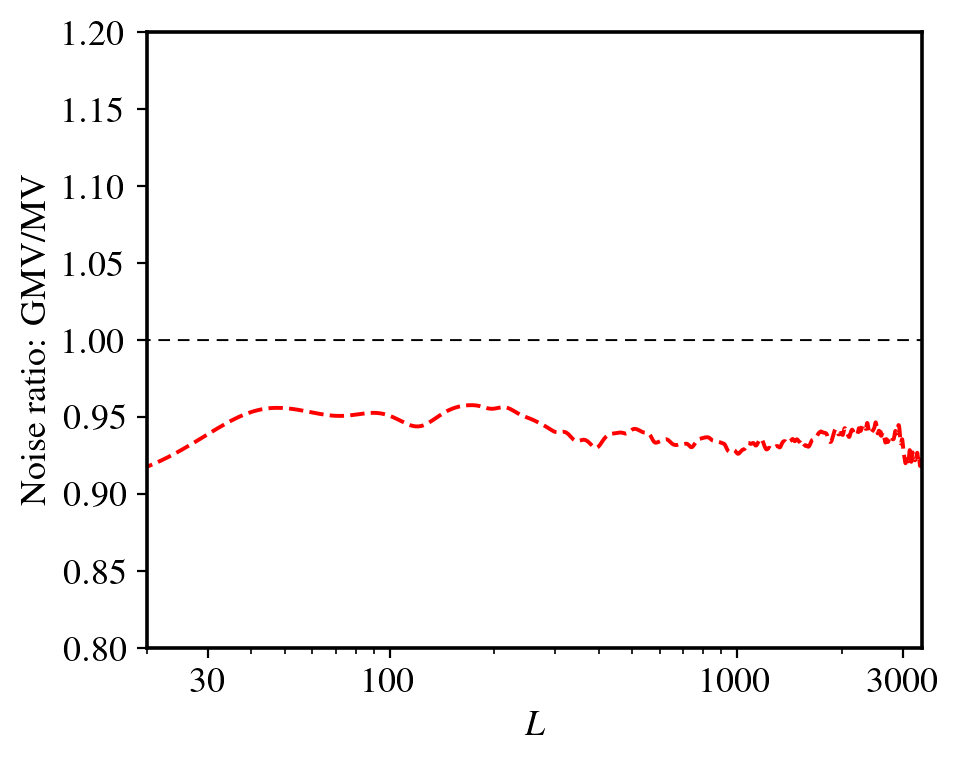
Global minimum variance

\phi_{LM}^{\rm GMV}\propto\sum_{\ell_{1}m_{1}\ell_{2}m_{2}} (-1)^{M} \begin{pmatrix} \ell & \ell' & L\\ m & m' & M \end{pmatrix} \bar{\bf{X}}_{\ell_{1}m_{1} } {\textnormal W}^{\phi}_{\ell_{1}L\ell_{2} } \bar{\bf{Y}}_{\ell_{2}m_{2} }
\phi_{LM}^{\alpha}\hspace{0.1cm}\propto\sum_{\ell_{1}m_{1}\ell_{2}m_{2}} (-1)^{M} \begin{pmatrix} \ell & \ell' & L\\ m & m' & M \end{pmatrix} \bar{X}_{\ell_{1}m_{1} } { W}^{\phi,{\alpha}}_{\ell_{1}L\ell_{2}} \bar{Y }_{\ell_{2}m_{2} }
\hat{\phi}^{\rm MV}_{LM}=\frac{\sum_{\rm \alpha}\hat{\phi}_{LM}^{\alpha} \mathcal{R}_{L}^{\phi{\alpha}} }{ \sum_{\alpha}\mathcal{R}_{L}^{\phi{\alpha}} }

SQE:

GMV:

Method based on Maniyar et al. 2021

\bar{X}, \bar{Y } \in \{ \bar{T}, \bar{E}, \bar{B} \}
\alpha \in \{ TT, EE, TE, TB, EB, ET, BT, BE \}
\bf{ \bar{X}}, \bf{ \bar{Y} } = \begin{bmatrix} \bar{T} \\ \bar{E} \\ \bar{B} \\ \end{bmatrix}

Allows us to use all the correlation info

~5% improvement on all scales

Foreground treatment

Our large-scale modes are dominated by  polarization so we are less prone to bispectrum (                      ) type biases. We nonetheless characterize contamination level by running different estimators.

\kappa_{\rm true}\times \kappa_{TT}

Y. Nakato

(Stanford)

clusters

radio/IR

clusters

radio/IR

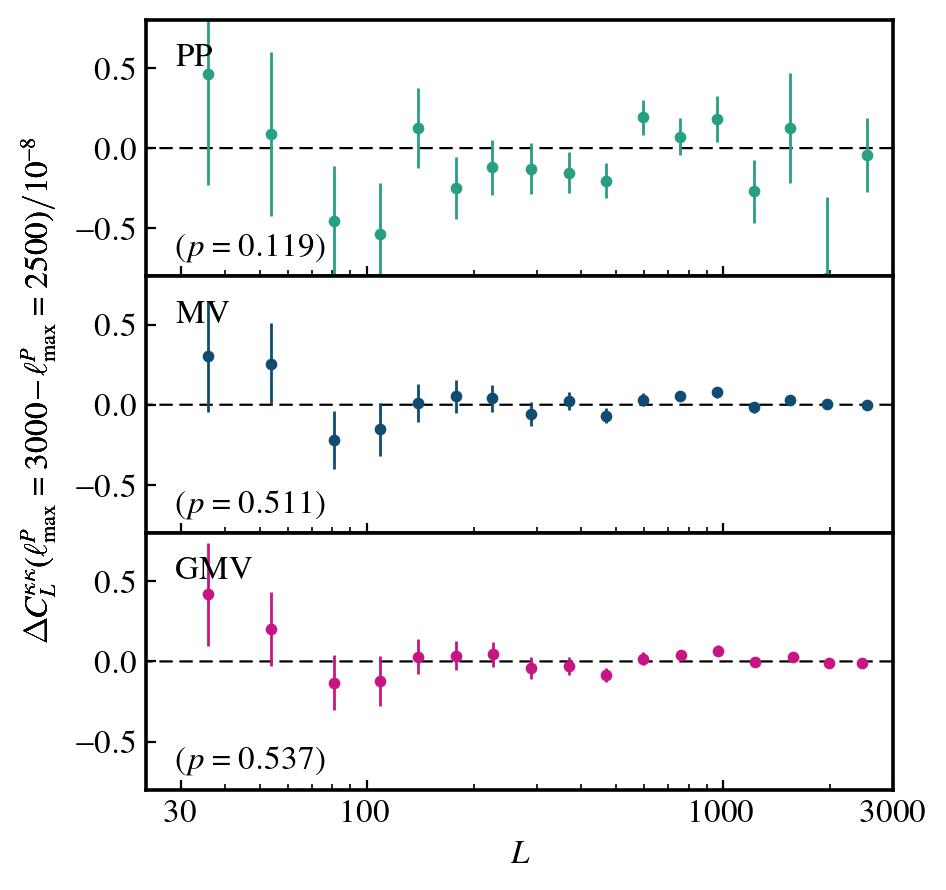
Consistency tests

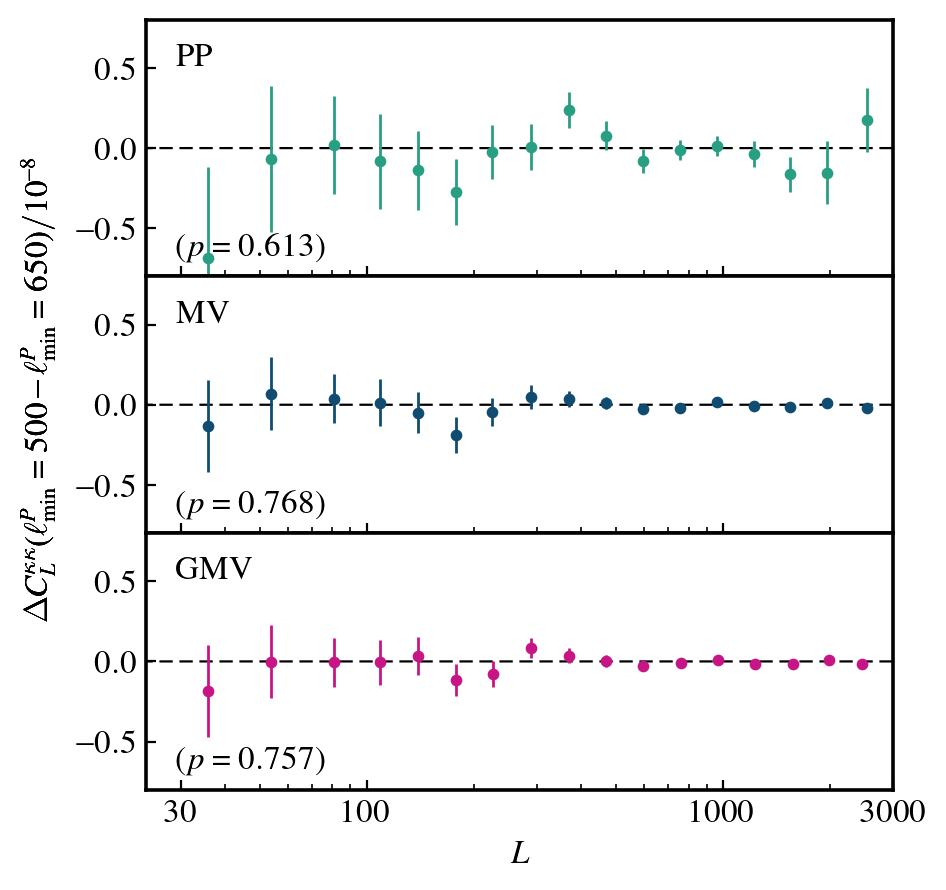
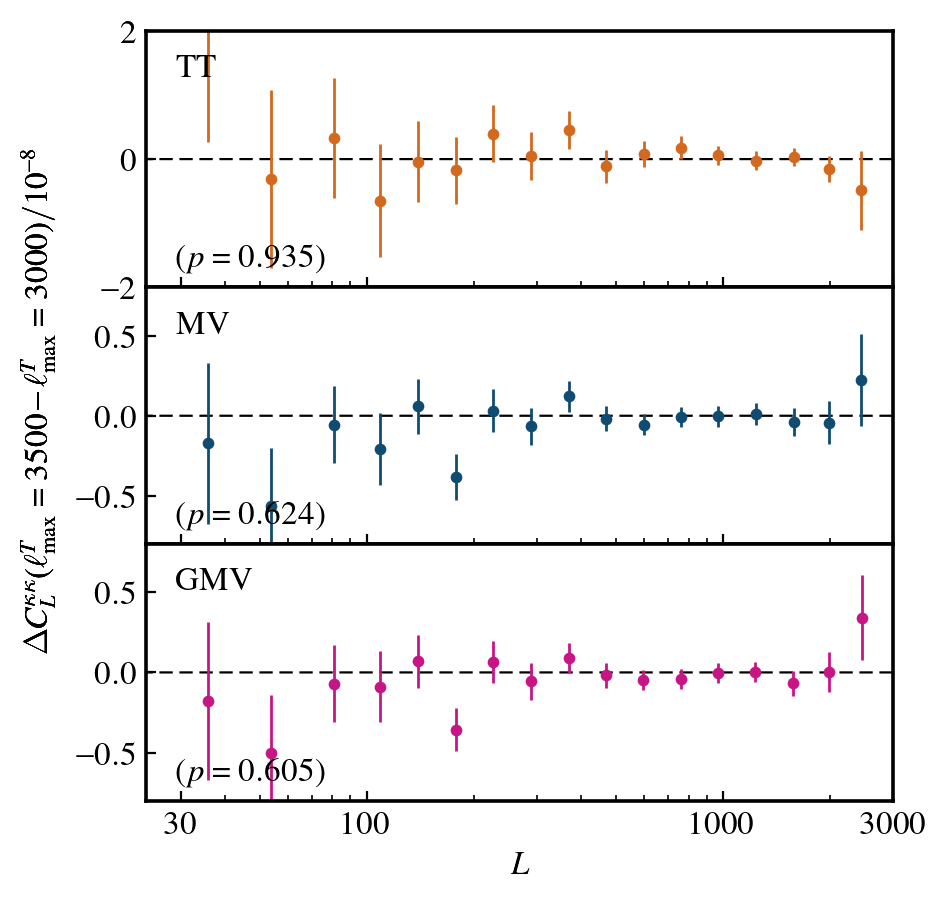
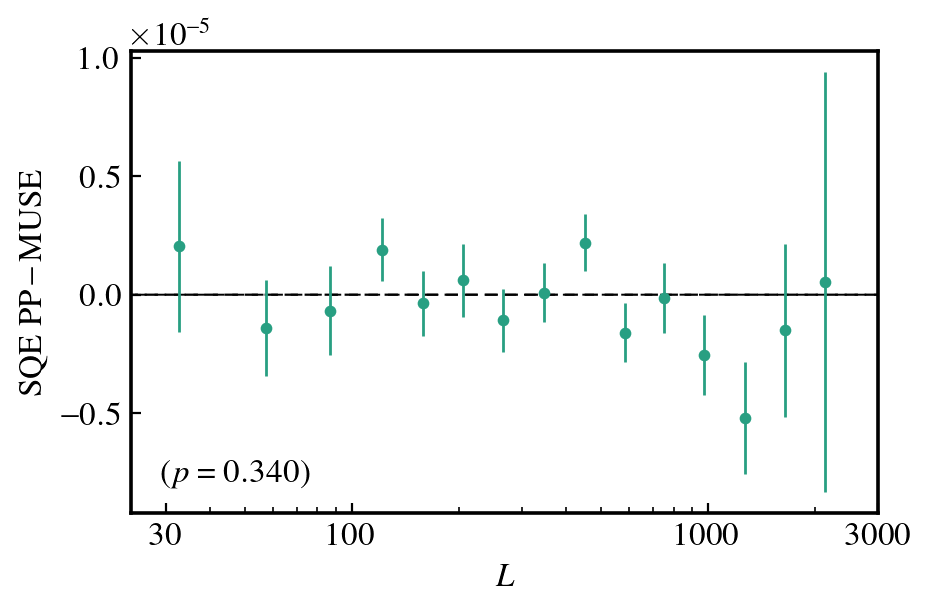
Polarization only

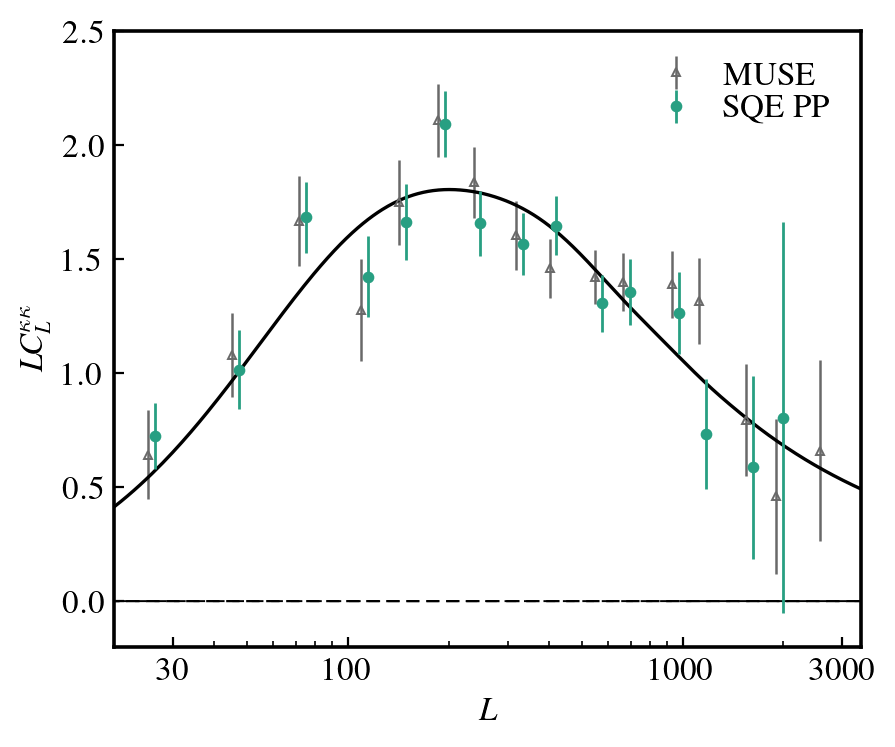
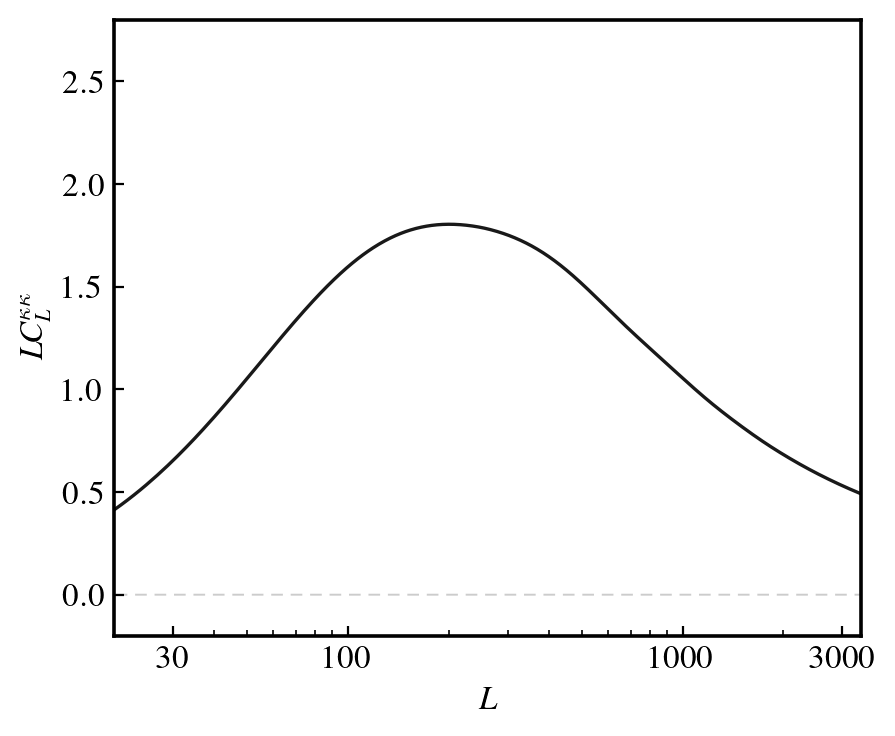
Power spectra

 Comparable uncertainties at L~250

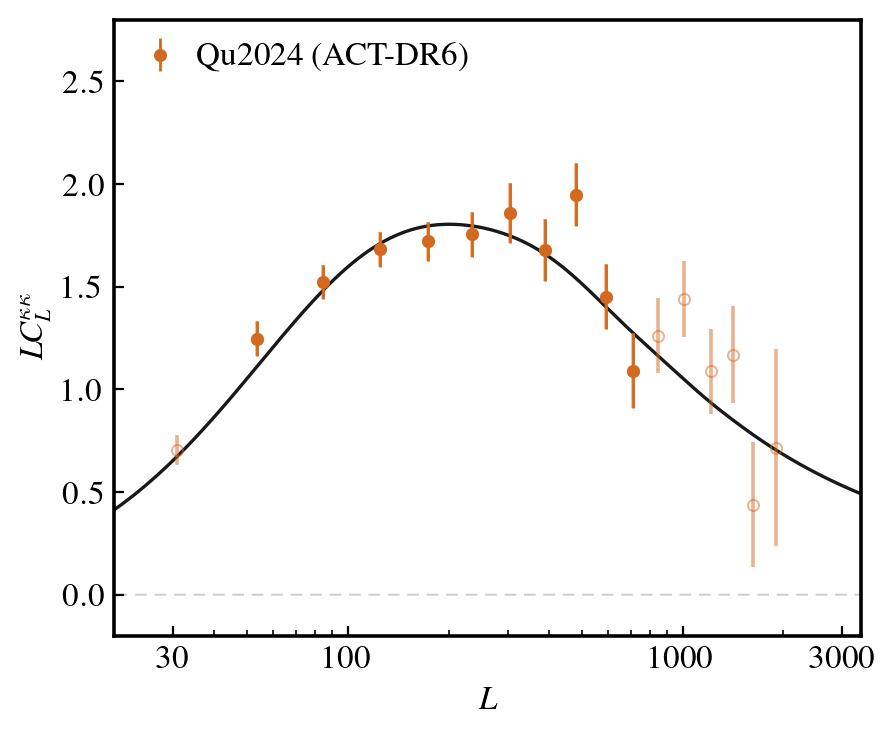
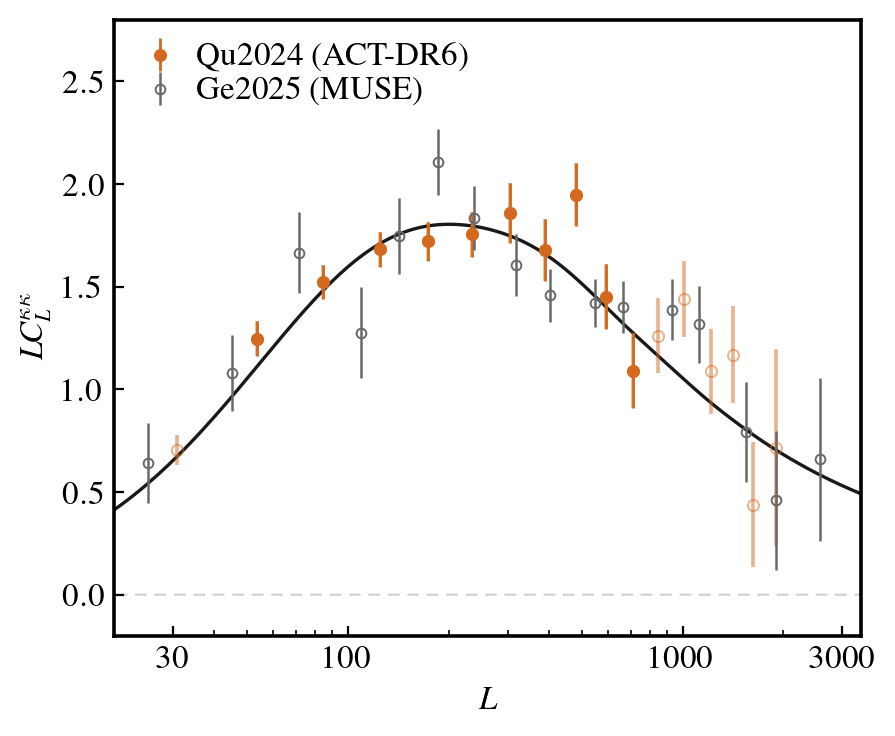
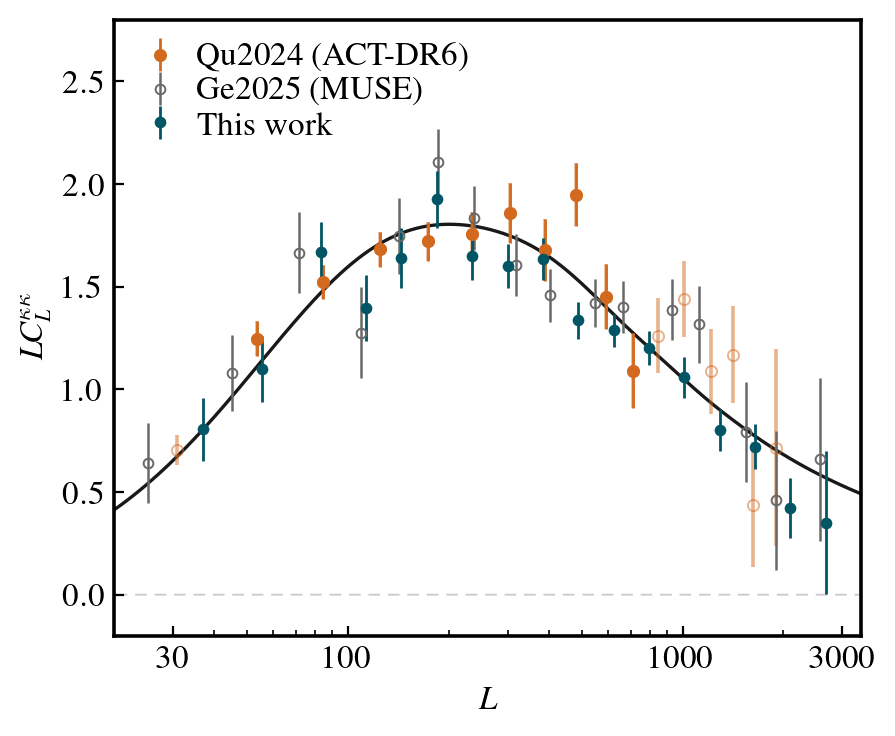
See Frank's talk

on Fri @9:20

See Fei's talk

on Thurs @9:20

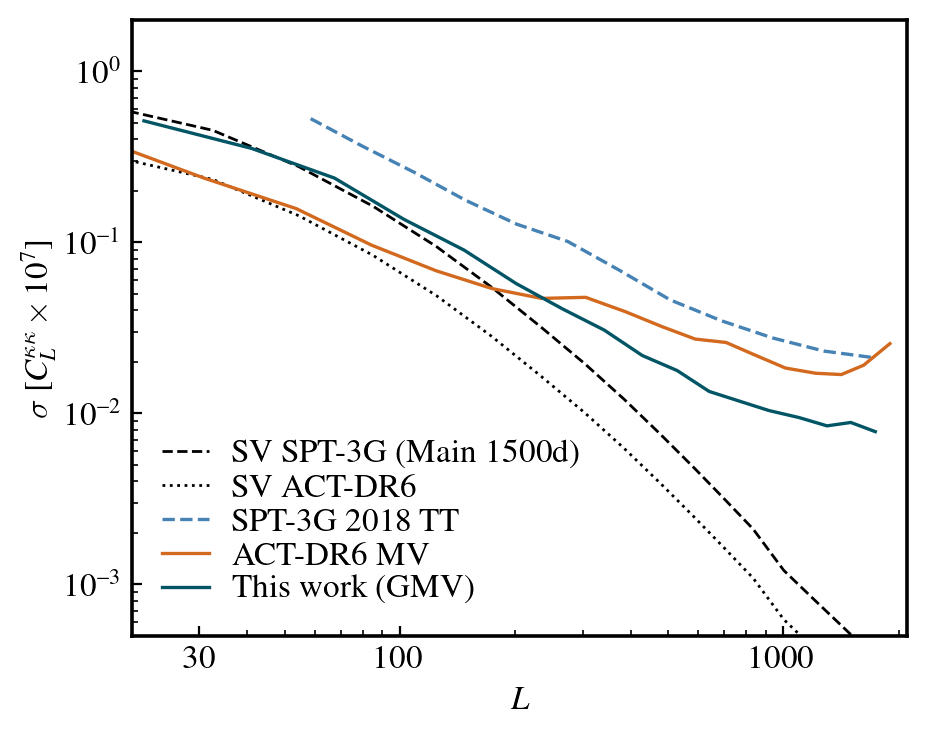
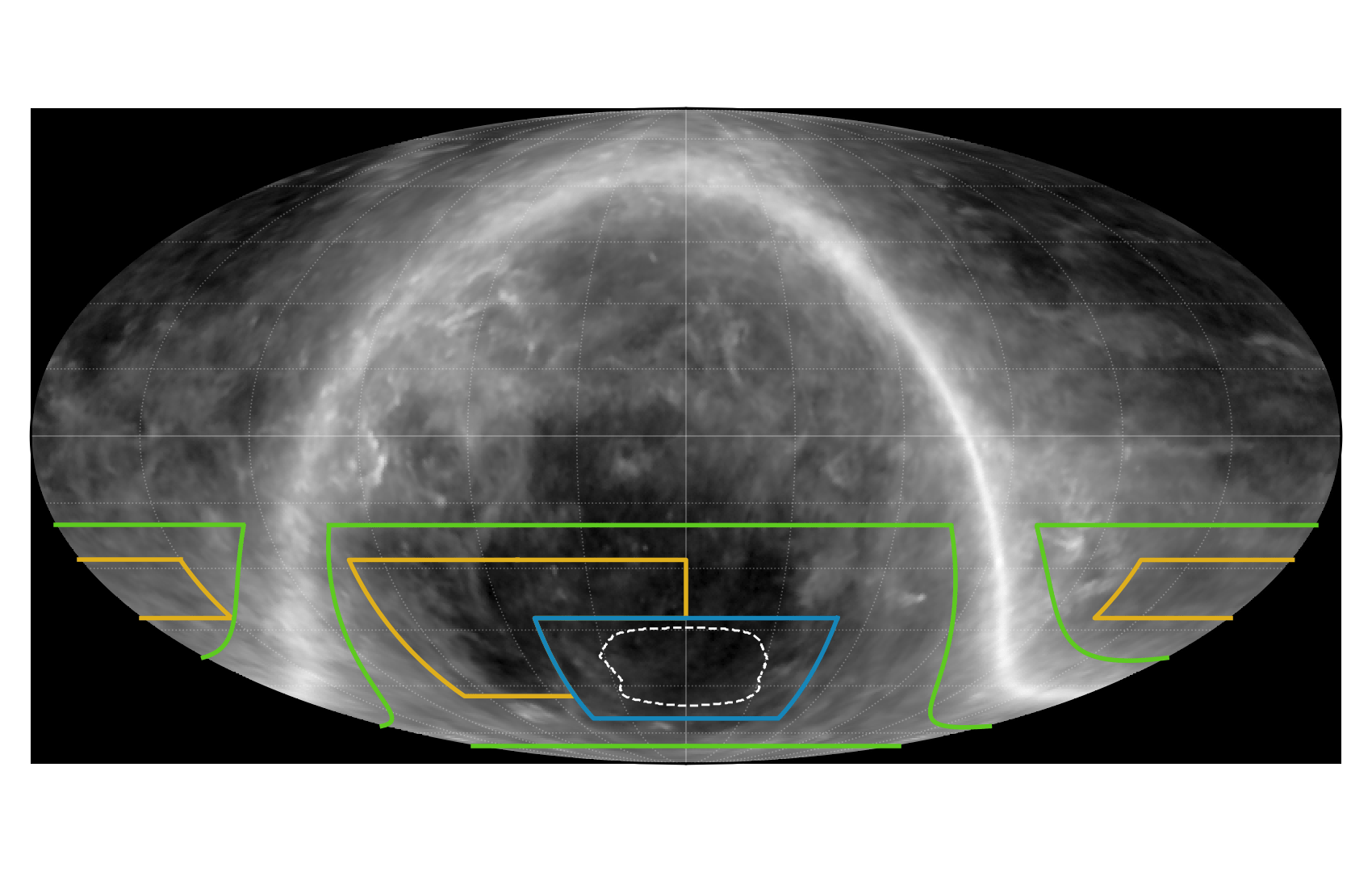
Larger footprint  coming soon

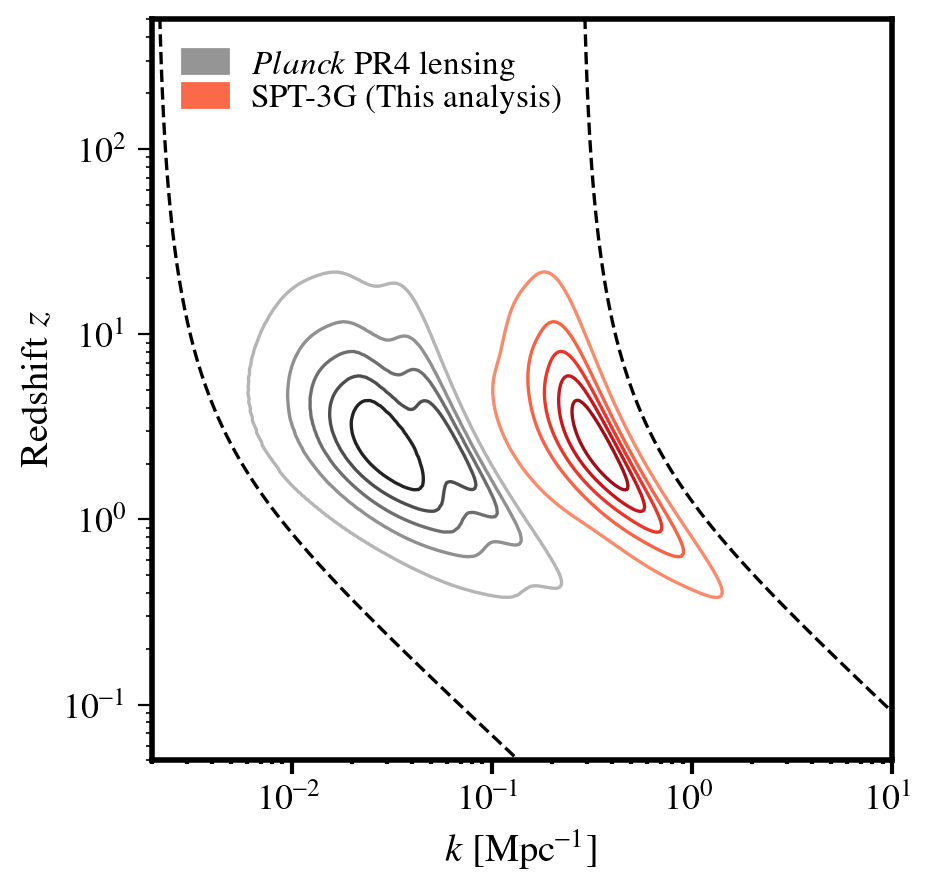
Scale sensitivity

  • Lensing map from this analysis probes significantly different scales compared to Planck's lensing map.
    • Scales above k = 0.1  contribute most to the total SNR.
       
  • Provides an unique handle  to  S8  at these scales + redshift and a way to check consistency/discrepancy from primary CMB predictions.  
{\rm Mpc}^{-1}

Systematic marginalization

We marginalize over 14 systematic parameters including:

  • - Tcal/Pcal (2 params)

  • - Beam (4 params)

  • -         (3 params)

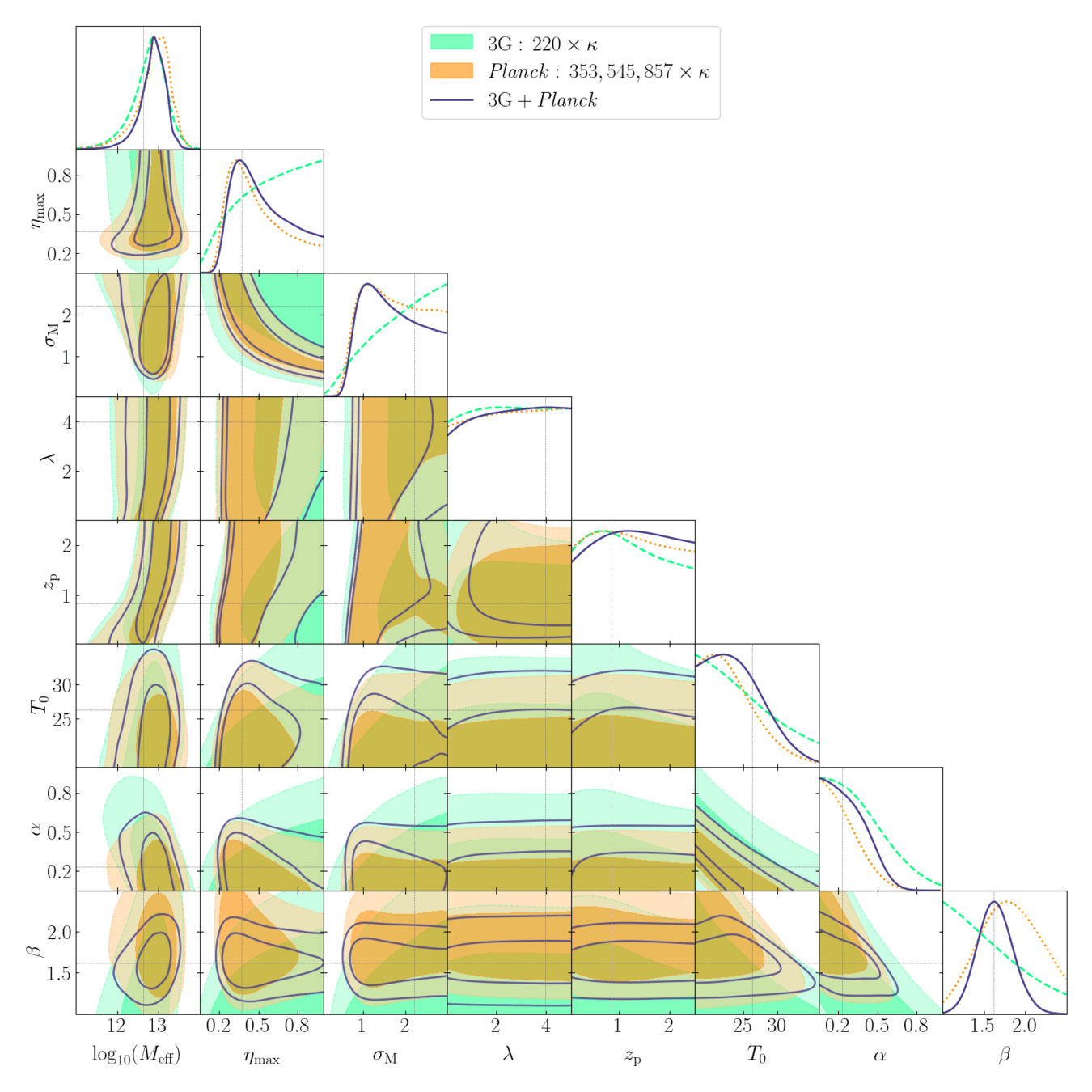
  • - Foreground (tSZ/CIB/radio; 5 params)

    • Atsz, Acib150, Acib220, Arad90, Arad150 applied to templates from the Agora simulation.

Computed using an emulator using GPJax and likelihood built on Candl to guarantee differentiability.

\beta_{\rm pol}

https://github.com/Lbalkenhol/candl

Mock constraints

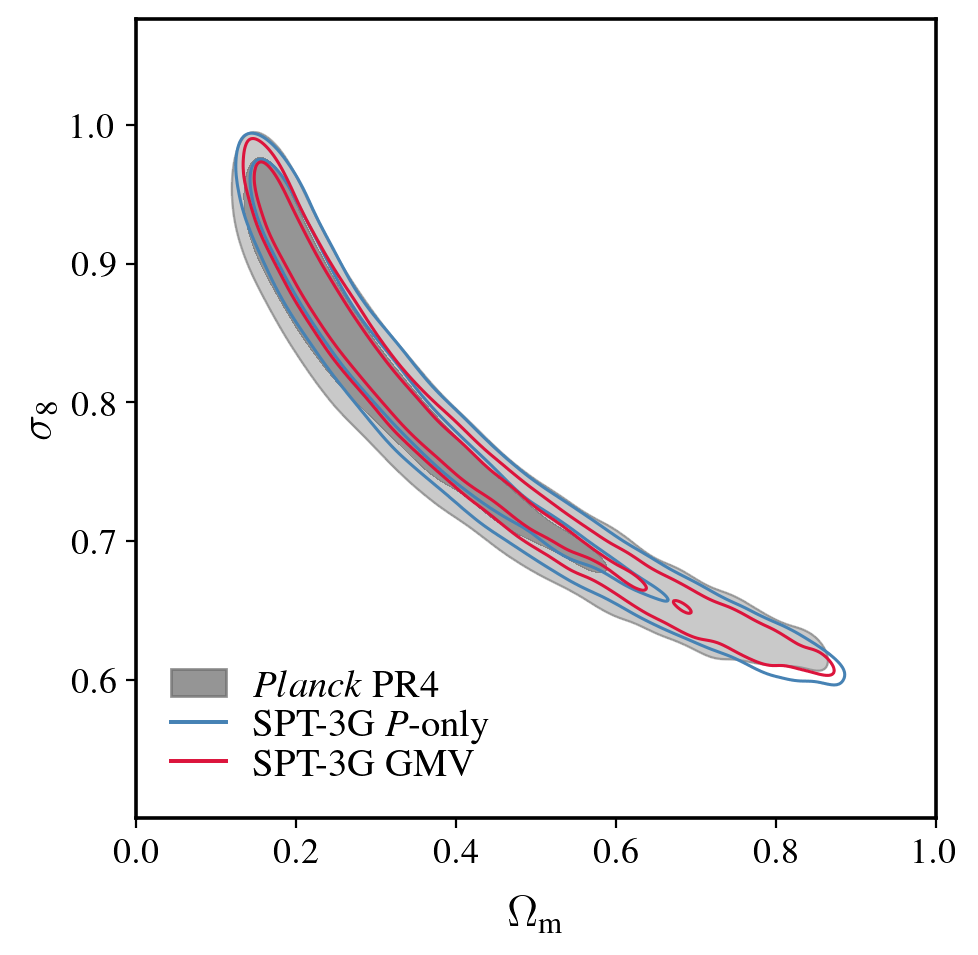
Planck: \Delta(\sigma_{8}\Omega_{\rm m}^{0.25})\sim2.7\%\\ {\rm ACT}: \Delta(\sigma_{8}\Omega_{\rm m}^{0.25})\sim2.7\%\\ {\rm SPT}\textnormal{-}{\rm 3G\ MUSE\ (P)} : \Delta(\sigma_{8}\Omega_{\rm m}^{0.25})\sim1.9\%\\ \textnormal{SPT-3G QE (P)}: \Delta(\sigma_{8}\Omega_{\rm m}^{0.25})\sim2.7\%\ (2.2\%\ no\ sys.)\\ \textnormal{SPT-3G QE (GMV)}: \Delta(\sigma_{8}\Omega_{\rm m}^{0.25})\sim1.7\%\ (1.4\%\ no\ sys.)

Lensing best constrains the parameter

combination 

\sigma_{8}\Omega_{\rm m}^{0.25}
\sigma_{8}\Omega_{\rm m}^{0.25}

Simulated

SPT-3G lensing x CIB

Karia Dibert

(U.Chicago > Caltech)

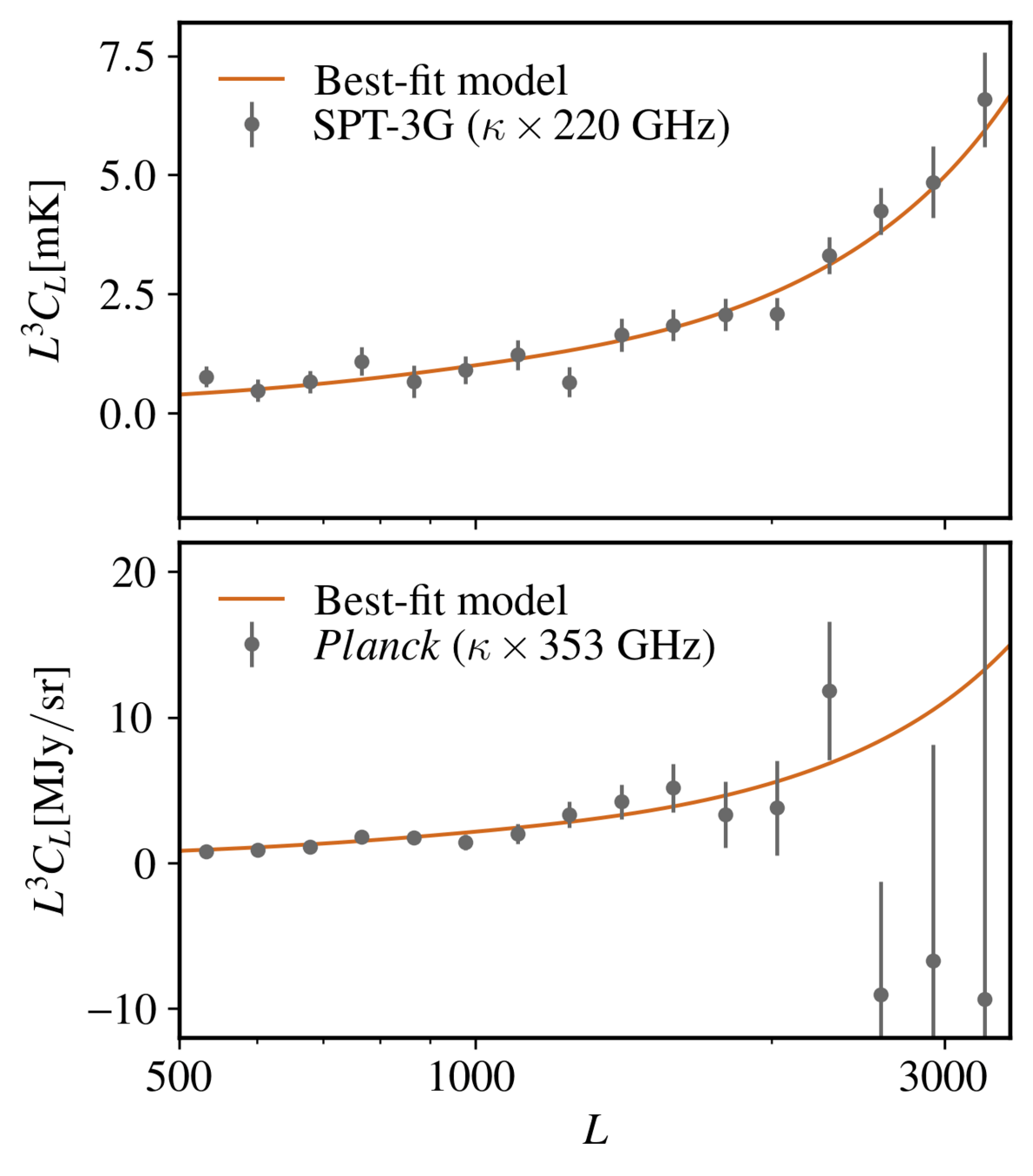
Preliminary

Wide field survey

K. Levy

(U. Melbourne)

S. Raghunathan

(UIUC)

Y. Li

(U. Chicago)

Y. Nakato

(Stanford)

Future SPT-3G lensing maps

J. Carron

(U. Geneva)

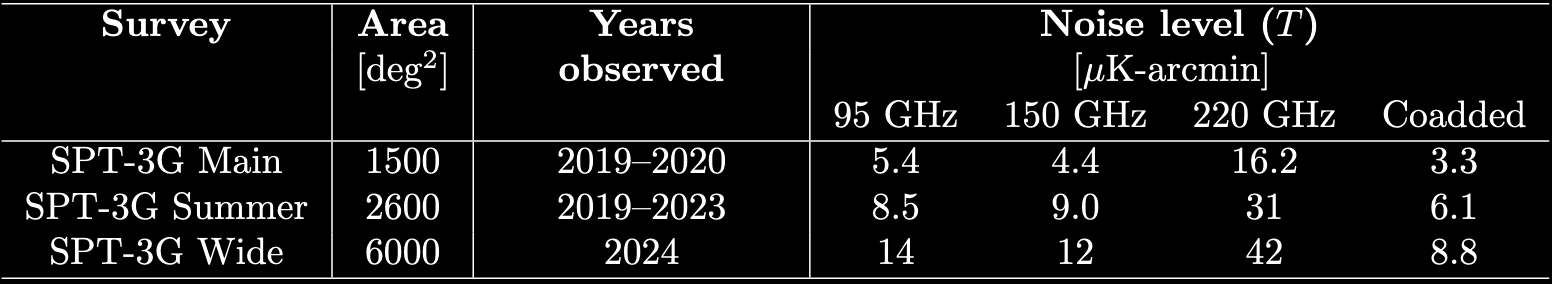
Cross-correlations

DES

Rubin

Euclid

A. Carolina Silva Olivera

(Stanford)

A. Ouellette

(UIUC)

C. Dailey

(Saclay)

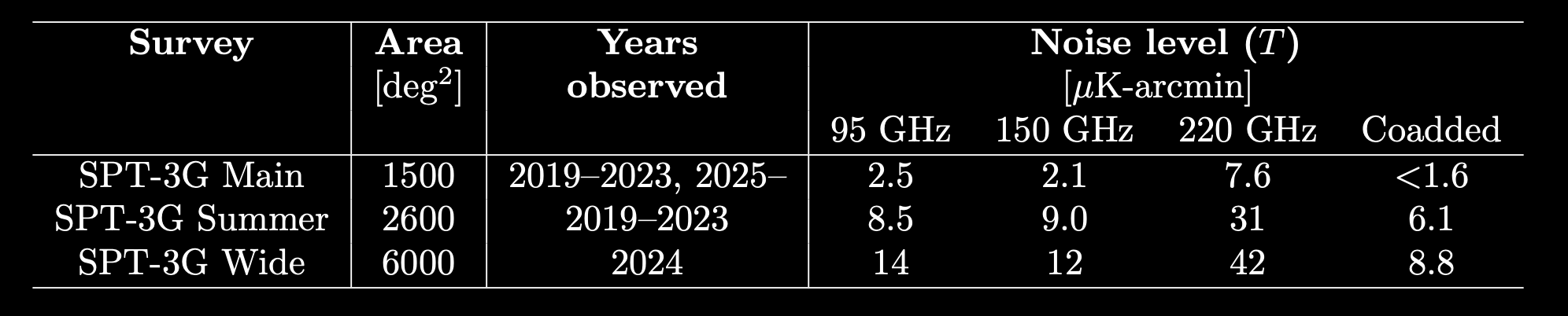
NSF-DOE Vera C. Rubin Observatory

x tSZ

x shear

x Euclid

(U.Chicago > Caltech)

Karia Dibert

x CIB

Summary

  • The SPT-3G main survey delivers deepest maps of the cosmic microwave background in the sub-degree scales enabling powerful constraints on cosmology from just ~3.5% of the sky.
     

  • CMB lensing measurements powered by these maps probe structure growth in the mildly non-linear regime, exploring scales previously little constrained —> weigh in on  S8 tension.
     

  • Uncertainty on               is forecasted to be almost 40% tighter than those from Planck’s and ACT’s lensing measurements.
     
  • Combining with TT/TE/EE measurements, we provide competitive constraints on LCDM parameters (coming soon).
\sigma_{8}\Omega_{\rm m}^{0.25}